Burp Sequencer 101

Talking to a friend the other day, I realised that some smart hackers who use Burp Sequencer for analysing session token randomness do not necessarily realise quite how it works or how to interpret its results.

This is hardly surprising: statistical testing for randomness is a complex business; Burp Sequencer lets you click and go; and all hackers like a tool which they can whip out and use without too much effort.

Anyone who really wants to understand the inner workings of Burp Sequencer can of course read TFM. But for everyone else, here are four key questions that you should know basic answers to if you want to use the tool effectively.

1. What does "bits of effective entropy" mean?

Each token is a collection of individual bits of data. Burp converts each token into a bit-level representation based on the size of the character set that appears at each position within the raw token - for example, if the first character position employs 8 different characters, then this represents 3 bits of data.

Burp tests each bit position within the token separately. If you have captured 1,000 tokens for analysis, then Burp tests the 1,000 values at the first bit position; then the 1,000 values at the second position; and so on. Several different tests are performed, and an overall result is derived for each bit position. Because the different tests look for different statistical features of non-random data, the "score" for each bit position is the lowest score returned by all of the tests. In other words, if a bit position fails any of the statistical tests, then that bit position is deemed to be non-random, and so fails overall.

(Burp also tests for correlations between the data at different bit positions, to avoid perverse results in cases where the same data is duplicated at different points within the token.)

2. What does "significance level" mean?

Burp reports an overall result showing the quantity of effective entropy "at a significance level of 1%":

and also shows a chart showing the amount of entropy at other significance levels:

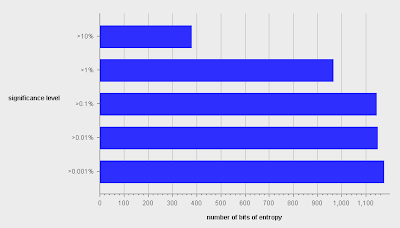
Unless you enjoyed statistics at school, don't dwell on this. The significance level represents how stringent we want our tests to be in identifying non-random data. The lower the significance level, the more obviously non-random a sample needs to be before we reject the conclusion that it is random. 1% is a common, and reasonable, significance level to use in this kind of test - it means roughly that we will wrongly conclude that random data is non-random in only 1% of cases.

So the "Overall result" at the top of the Summary tab is the right one to use in general.

3. How many samples do I need to capture?

This is a very important question. In many situations, capturing a large sample of tokens from a web application may be time-consuming or intrusive. As a convenience, Burp lets you perform the statistical tests based on a sample of only 100 tokens. The only use for this is to allow you to quickly identify tokens that are blatantly non-random. Getting a "pass" result based on this size of sample provides very little assurance of the actual statistical properties of the token generator. The "Reliability" message at the bottom of the Summary tab gives you a rough indication of how effective your sample size is:

In general, unless smaller samples prove obviously non-random, you should aim to capture at least 5,000 tokens from the application, and more if possible. To see why, let's look at the results of testing a defective token generator. Suppose an application uses the following broken linear congruential generator:

long nextToken = lastToken * 13 + 27;

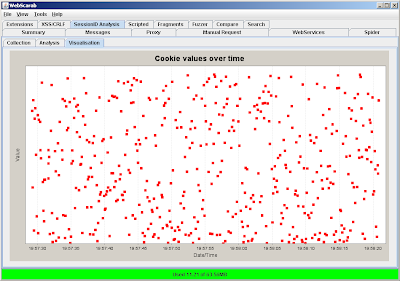
Although broken, this generator produces tokens that look fairly random to the naked eye, as evidenced by WebScarab's graphical view:

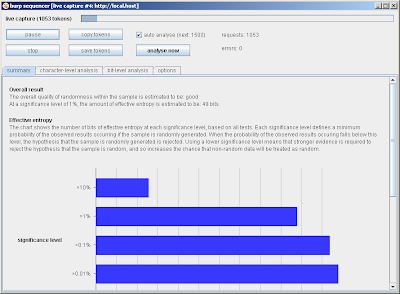
After capturing 1,000 tokens using Burp, the statistical tests report 49 bits of effective entropy: a "pass" result in most situations:

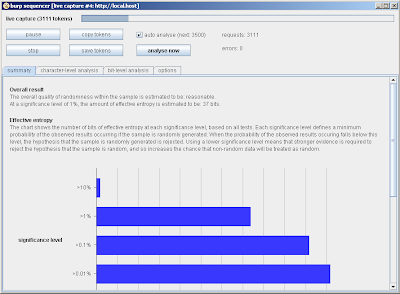
However, if we continue and analyse 3,000 tokens, the result is less promising: only 37 bits pass the tests:

And after analysing 6,000 tokens, only 17 bits pass the test: a "fail" result in most situations:

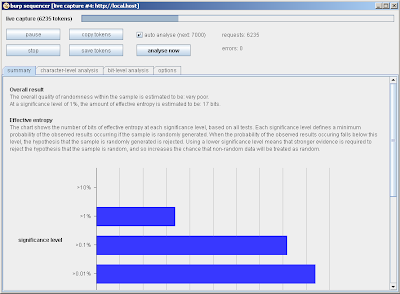
Continuing further, Burp will eventually report that all bits fail the test. So to reiterate: size really matters. The non-random properties of many generators only emerge when large sample sizes are tested. If in doubt, always continue capturing.

4. How does Burp's result relate to predictability?

Statistical tests for randomness cannot in general establish predictability or otherwise. Deterministic data may pass statistical tests for randomness and yet be completely predictable by someone who knows the generation algorithm (for example, a hash of an incrementing number). Conversely, data that fails statistical tests may not actually be predictable in a practical situation, because the patterns that are discernible within the data do not sufficiently narrow down the range of possible future outputs to a range that can be viably tested.

In general, you should interpret Burp Sequencer's output as follows:

• If a large sample fails the tests, then the generator is definitely non-random, and its output may or may not be predictable in practice.
• If a large sample passes the tests, then the generator may or may not be random, and its output may or may not be predictable in practice.

I hope this helps clear up a few uncertainties people may have about using Burp to test for randomness. If you have any other questions, ask away.

session tokens burp

Dafydd Stuttard

@DafyddStuttard